

In the real world we come across various signals, some of them are measured by changes in resistance and some of them are with inductance and capacitance. If we consider the resistance, most of the industrial sensors like temperature, strain, humidity, displacement, liquid level, etc. produces the change in value of the resistance for a variable change. Therefore, there is a need for a signal conditioning for every resistance sensor.

Generally the resistance measurement is divided into three types, low resistance measurement, medium resistance measurement and the high resistance measurement. If the resistance measurement is possibly from a few milliohms to micro ohms, then it is considered as a low resistance measurement.
This measurement is actually used for research purpose. If the measurement is from 1 ohm to 100 k is generally referred as a medium resistance measurement. Potentiometer, thermistors, etc. measurement comes under this category. And very high resistance measurement is considered from 100 kilo ohm to greater than 100 mega ohms. For finding the medium value of the resistance different methods are used, but mostly Wheatstone bridge is used.
It is the most common and simplest bridge network to find the resistance is the DC Wheatstone Bridge. This bridge is used where small changes in resistance are to be measured like in sensor applications. This is used to convert a resistance change to a voltage change of a transducer.
The combination of this bridge with operational amplifier is used extensively in industries for various transducers and sensors. A Wheatstone bridge consists of four resistors that are connected in the shape of a diamond with the supply source and indicating instruments as shown in figure.
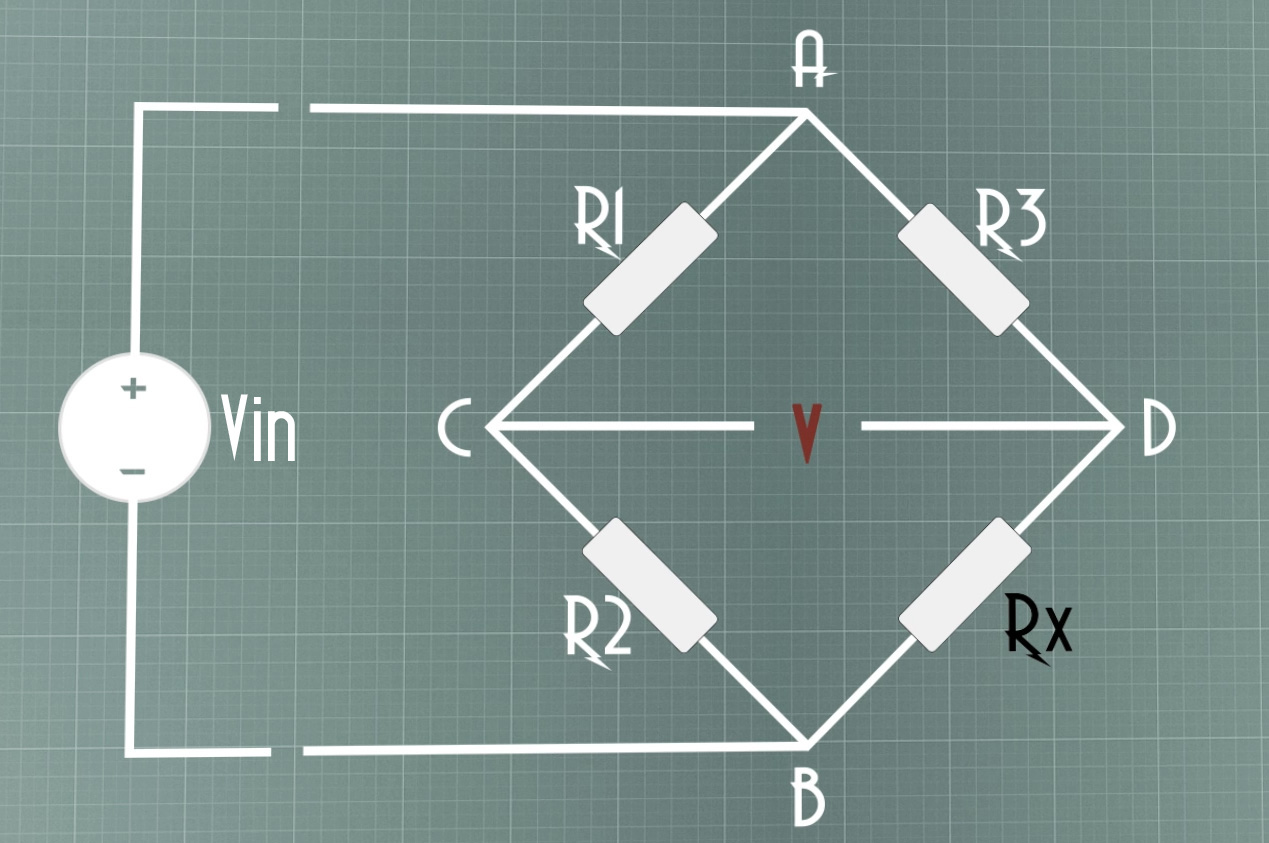
This bridge is used to find the unknown resistance very precisely by comparing it with a known value of resistances. In this bridge null or balanced condition is used to find the resistance. For this bridge balanced condition voltage at points C and D must be equal. Hence, no current flows through the galvanometer. For getting the balanced condition one of the resistors must be variable.
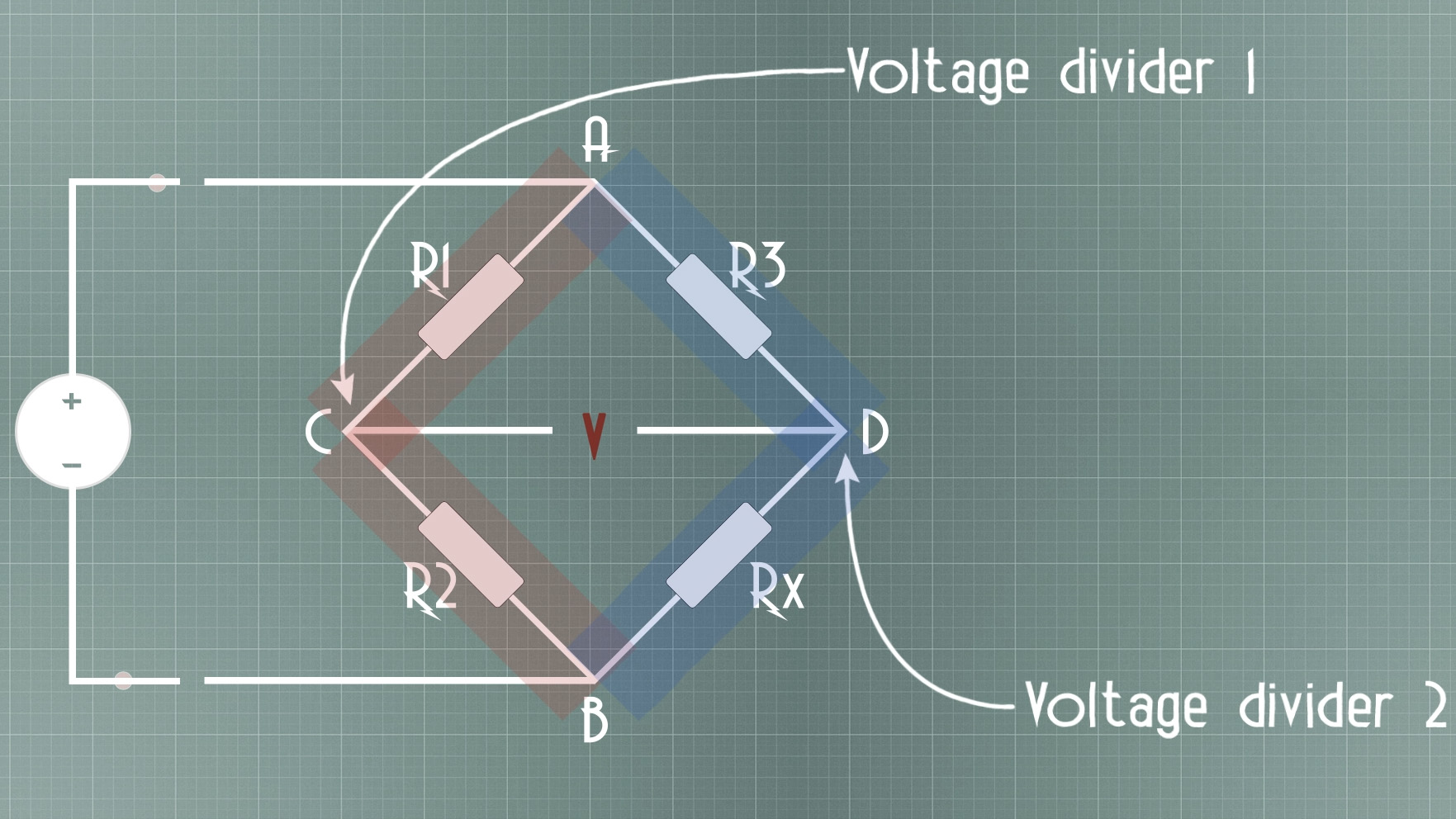
So, now the voltage between C and D is the voltaghe on D minus the voltage en C. We haev the formulas for each above so all we have to do is to make VD - VD. So:
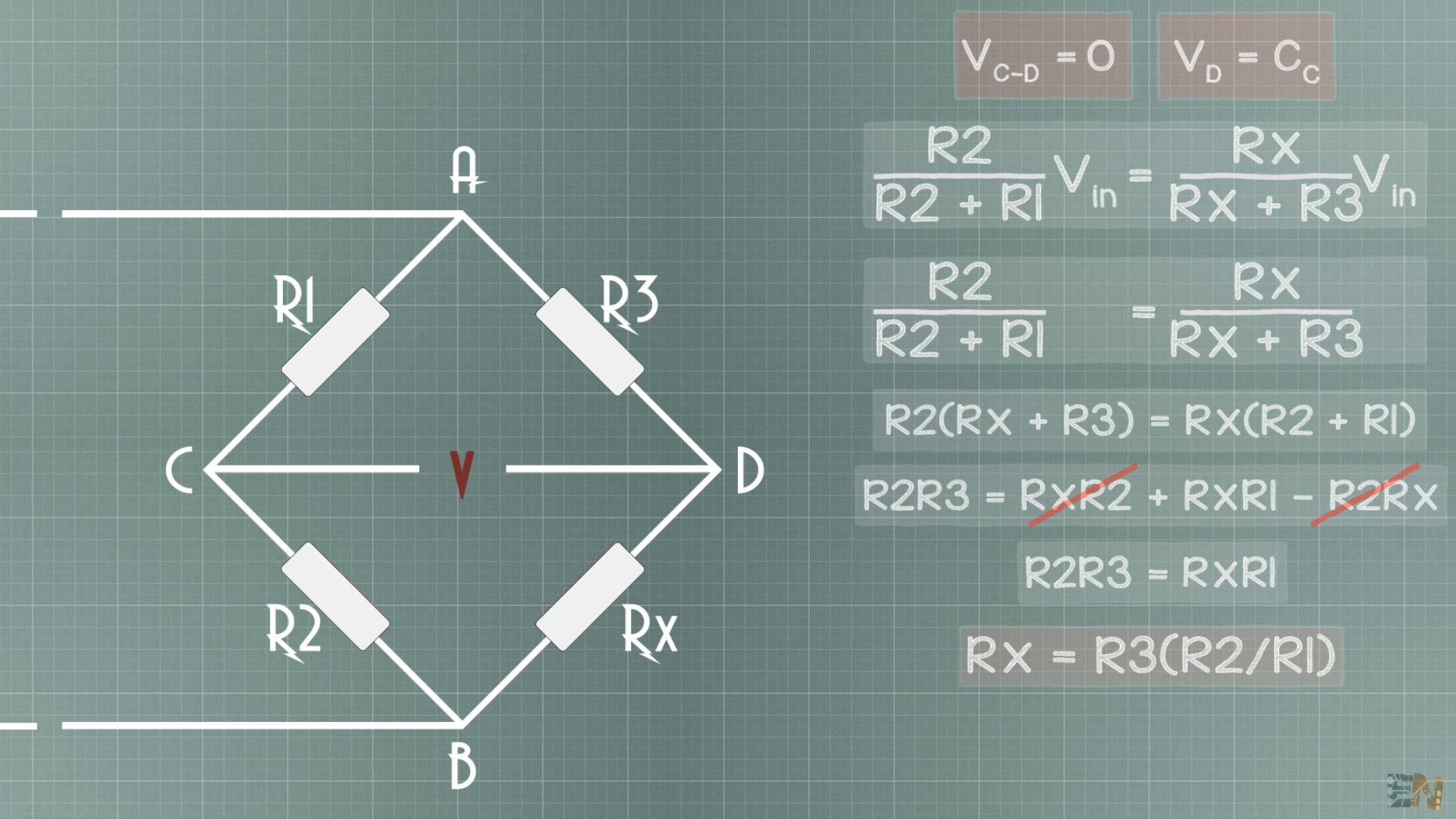
But, very important. What we look for is a balanced bridge. That is when VCD = 0V. So,now we imply that to out equation, VC - VD = 0; And then we can get what value should Rx have in order to get a balanced bridge.
From the above equation R4 or Rx can be computed from the known value of resistance R3 and the ratio of R2/R1. Therefore, most of the cases R2 and R1 values are fixed and the R3 value is variable so that null value is achieved and the bridge gets balanced.
So, as an example we connect a strain gauge instead of Rx to our Bridge. Let’s give values. On one side we have let’s say two resistors of 20 ohms and the supply is 10 volts. Using the divider formula, we get that the voltage on C is 5V. We change R3 resitance till we get 5V as well on point D and let's sat taht the gauge is 20 ohms as well.
This gauge will increase its resistance under forces. In practice, the range of strain gauge resistance is from 30 ohms to 3 thousands ohms. For a given strain, the resistance change may be only a fraction of full range. Therefore, to measure a fraction of resistance changes with high accuracy, Wheatstone bridge configuration is used.
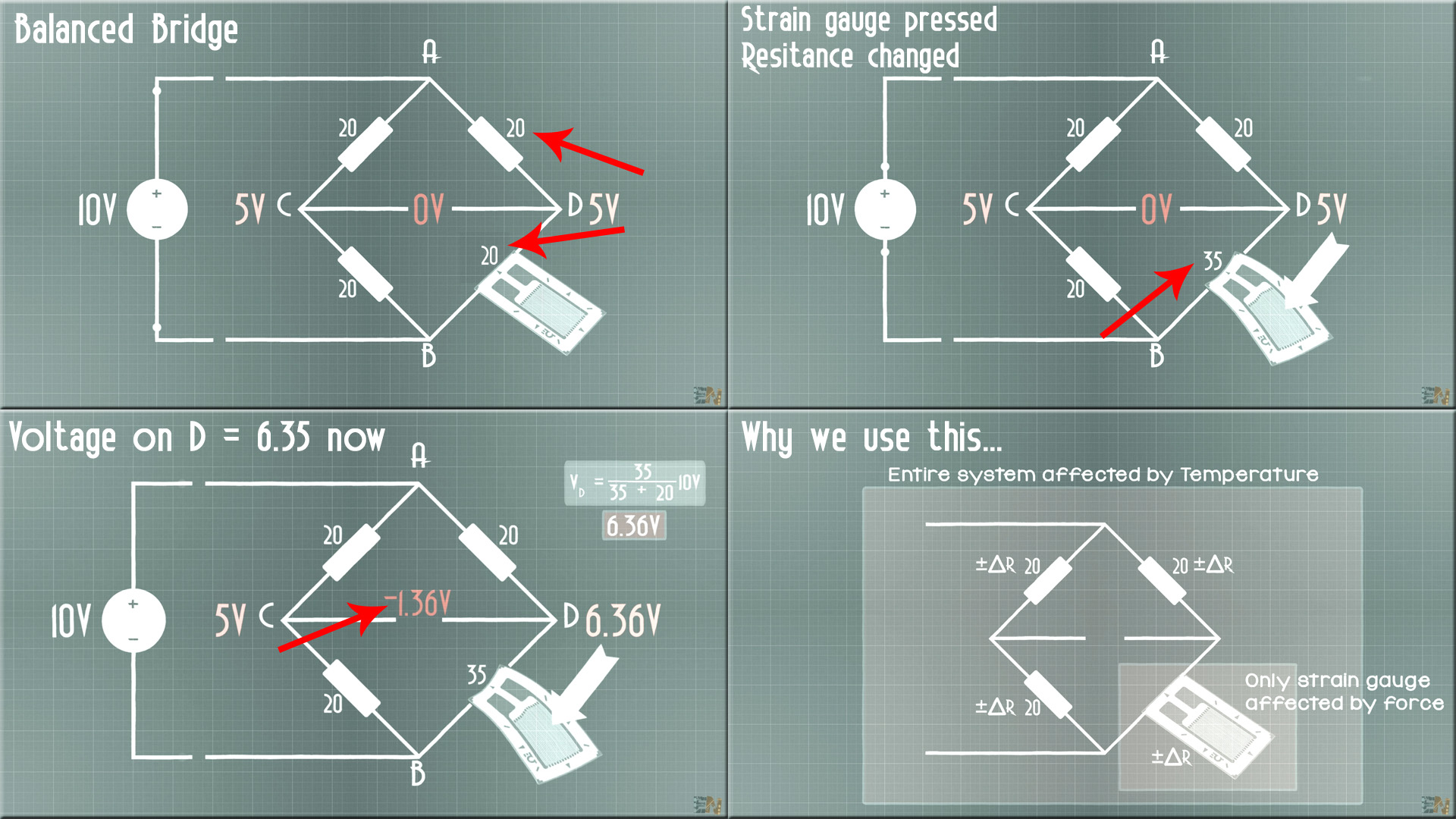
First step, the bridge is balanced so we have CD equal to 0 volts. We apply force on the gauge and the resistance is getting bigger so the voltage drop on the gauge is now bigger. Let’s say the gauge is now 35 ohms. The voltage on D would now be 6.36 volts so the voltage on CD is negative 1.36 volts. So, we pass force measurements to very small resistance changes and then to voltage values so we could use this in our projects, maybe connect it to a microcontroller.
But now you might wonder, why not use the gauge directly with a voltage divider? Well, this kind of sensors might change their resistance by other factors as well as for example temperature. Let’s say that we apply force on the gauge and we measure 20 ohms in a room of 30 degrees. Then we apply the same force but in a room at 50 degrees and we get 18 ohms. That means that the gauge read is not reliable because it will change with the temperature as well and we don’t want that.

But if we put this in a Whetstone bridge together with other resistors that will also change by the temperature, the output won’t be affected because the entire system is affected by temperature but only the gauge is affected by force so we separated temperature error from the gauge sensor. We could use this setup with gauge sensors, light dependent resistors or thermistors so we could measure forces, light or temperature. It is a basic circuit and very easy to understand.
1. The Wheatstone bridge is used for measuring the very low resistance values precisely.
2. Wheatstone bridge along with operational amplifier is used to measure the physical parameters like temperature, strain, light, etc.
3. We can also measure the quantities capacitance, inductance and impedance using the variations on the Wheatstone bridge.